How To Use A Digital Camera To Propose

Abstruse

In this paper we bargain with the problem of digital camera identification by photographs. Identifying photographic camera is possible by analyzing camera's sensor artifacts that occur during the process of photo processing. The problem of digital photographic camera identification has been popular for a long fourth dimension. Recently many effective and robust algorithms for solving this problem accept been proposed. However, nigh all solutions are based on state-of-the-art algorithm, proposed by Lukás et al. in 2006. Core of this algorithm is to summate the and then-chosen sensor pattern noise based on denoising images with wavelet-based denoising filter. Such technique is very efficient, merely very time consuming. In this paper we consider tracing cameras by analyzing defects of their optical systems, like vignetting and lens distortion. We prove that assay of vignetting defect allows for recognizing make of the camera. Lens distortion tin can be used to distinguish images from different cameras. Experimental evaluation was carried out on threescore devices (meaty cameras and smartphones) for a total number of 12 051 images, with back up of the Dresden Image Database. Proposed methods practice not require denoising images with wavelet-based denoising filter what has a pregnant influence for speed of image processing, compared with state-of-the-fine art algorithm.

Introduction

The popularity of photography is obvious. Lots of people take photos with their smartphones or cameras and immediately share them in social media. It is clear that tracing cameras may expose users' privacy to a serious threat. Problem of tracing digital cameras has been popular for a long time. Tracing a photographic camera is understood as a recognition of camera's sensor. In [xi] procedure of searching for characteristic features for identifying the camera is chosen hardwaremetry. According to [13, 31] each camera leaves some specific and unique traits in the images that makes it possible to trace the photographic camera and could serve as a "photographic camera fingerprint". Such fingerprint is nearly frequently understood equally pixel artifacts resulting of sensor imperfections or defects of eyes. I of the classic and state-of-the-art algorithms for photographic camera recognition was presented by Lukás et al. in [31]. For each camera it is determined the so-called sensor pattern dissonance that acts as an unique camera fingerprint. This sensor pattern noise is calculated by averaging noise obtained from multiple camera's images using a denoise filter. According to the authors, efficiency of the algorithm depends on denoising filter used for processing the images and experimental evaluation showed that wavelet-based denoising filter achieves best results. Such approach is very constructive and the recognition of the camera is at very high level. All the same, using the wavelet-based denoising filter is very fourth dimension consuming [thirty]. Typical time for denoising 12 megapixel photo takes near two minutes; time for denoising 24 megapixel photograph takes three to even four minutes. It is clear that this issue makes usage of this approach for large sets of images impractical. Therefore, there is a motivation to consider methods that will be fifty-fifty less accurate, but much faster.

In this paper we talk over quite dissimilar approach in order to recognize the photographic camera. We are not because afore mentioned dissonance that tin can be extracted from images only typical defects of optical system, like lens baloney and vignetting.

Vignetting is a kind of fault that occurs due to optical defects or sensor imperfections [x, 34]. Information technology reveals as a reduction of image brightness at the edges of the image. Therefore, vignetted images take visually darker corners than rest of an image. Such defect is popular in lots of digital cameras (peculiarly compacts and digital single lens reflectives). Types of vignetting are precisely described in [10]. This topic has attracted many researchers, therefore a lot of algorithms [6, 22,23,24] and patents [27] for vignetting correction are developed. Lens distortion is a deviation from rectilinear projection [5, 32]. This miracle causes straight lines in the picture to become curved. Information technology is seen in the images as differences in magnification of the image depending on its altitude from the optical axis [14].

We analyze these defects in lodge to recognize camera's brand. The goal is to reduce the fourth dimension for processing the prototype in comparison to Lukás et al.'s method. To the best of our knowledge, nobody before has tried to utilize vignetting or lens distortion for tracing the camera.

Contribution

Contribution of this paper is twofold. First, nosotros clarify the vignetting defect in lodge to identify make of the camera. Nosotros examine reduction of photograph effulgence at the edges of a set of images with the same frame perspective. We experimentally show that there are some tendences of underexposed areas in the epitome edges that might be helpful to recognize camera's brand or even photographic camera's model. Secondly, we evidence that analyzing image baloney can likewise be used for distinguish two cameras. Proposed observations are less efficient in photographic camera's brand recognition compared with Lukás et al.'s algorithm [31] but significantly faster, what makes it practical to use them for processing large sets of images.

Organization of the newspaper

The paper is organized as follows. In Department 2 related and previous work is described. Department three describes the analysis of vignetting and lens distortion. In Department 4 experimental evaluation is presented. Final section concludes this work and points some future research directions.

Related and previous work

The issue of tracing cameras is studied in various ways. One of the well-nigh popular and considered as state-of-the-art work on camera sensor recognition is Lukás et al.'s algorithm [31]. This algorithm is in detail described in I. Authors proposed an algorithm for calculating camera's fingerprint which is based on a deviation betwixt prototype p and its denoised class F(p).

In [ii] we have proposed a fast method for camera tracing based on Peak signal-to-noise ratio. Method is very fast in comparison with [31], even so classification efficiency is lower.

In [one] authors proposed using the one thousand-means algorithm for managing photo response non-uniformity (PRNU) patterns. Patterns are compared to each other using correlation and grouped by k-means algorithm. Therefore, similar patterns grouped over a cluster are considered every bit belonging to the same photographic camera. Experiments were conducted for a database of 500 images. Images grouped within a cluster were with truthful positive rate (TPR) of 98% belonging to the detail camera. The idea of fingerprint clustering is likewise presented in [three].

In [20] analysis of JPEG pinch is carried out. It is well-known that JPEG lossy compression generates a noise that impacts groups of pixels. However, authors show JPEG compression adds some specific artifacts to the concluding prototype and the exact implementation details may be used for identification.

In [17] an approach of counterfeiting characteristic features of the camera in order to produce an image "pretending" to be done by another camera is presented. The technique is described as photo-response nonuniformity fingeprint-copy attack. The goal is to obfuscate sensor design noise of a detail photographic camera past "inserting" into it a sensor pattern racket of another camera. It is showed that this tin can be done by performing simple algebraic operations. Let us assume that \(\hat {K_{N}}\) is a camera fingerprint calculated of N images and J is a fingerprint of another camera whose we want to put into \(\hat {K_{N}}\). And then nosotros take \(J' = J(1+\alpha \chapeau {K_{Due north}})\), where a >0 is a scalar defining fingerprint strength. Experimental results testify that such "exchange" of camera fingerprints is very efficient, i.east. based on \(\hat {K_{N}}\) we tin produce a counterfeit photo \(J^{\prime }\) pretending that camera. Almost the same proposition is described in [35, 41]. This technique has a serious disadvantage, beacuse it may be impractical. It is required to have a representative image set of camera that we want to "substitution" a fingerprint with and affects the actual paradigm (i.east., the stored data). Due to denoising images, this method is also very time consuming.

In [4, 26, 29] expressionless pixels, pixels traps, indicate/hot signal defects and cluster defects were investigated in terms of camera recognition. Experimental results show that different cameras have a singled-out pattern of defective pixels, hence in some cases, hot and expressionless pixels allow recognizing the sensor.

In [21] a similar method as in [31] is presented. A sensor fingerprint is considered as a white dissonance present on the images. Authors advise using correlation to circular correlation standard as a test statistic, which may reduce faux positive rate (FPR) of camera recognition. However in dissimilarity to [31], authors examine proposed method on fragments of photos instead of "full" photos. The true positive rate of recognition was 95% (fragments of size 256x256px) and 99% (512x512px).

In [13] a technique based on cross-correlation analysis and tiptop-to-correlation-energy (PCE) ratio to identify the camera is proposed. Sensor pattern noise is calculated and the correlation detector with PCE ratio to measure the similarity betwixt noise residuals is used. Even so, time performance is not examined.

In [18] a method for camera identification using correlation is presented. Authors consider existing database with different cameras' fingerprints and calculate correlation coefficient of a fingerprint of a new camera for comparison. This approach is clearly based on Lukás et al.'southward algorithm, moreover authors practise not depict, how database of fingerprints is gained.

In [39, 40] a gradient technique for vignetting correction is described. It is as well pointed that vignetting tin can be described by natural image statistics. In [23,24,25] polynomial models for vignetting correction are proposed.

In [32] ii methods for calculating lens distortion in order to camera calibration are presented. Offset method is based on look-up-tables (LUT) of focal length and lens distortion. 2nd method uses relationships between some characteristic points found in paradigm. Calculation of lens distortion is done by algebraic operations.

Piece of work [28] presents a method for camera calibration and radial distortion correction. Radial distortion tin be calculated past two distorted images. Advantage of this method is that no knowledge virtually camera'due south intristic paramters nor scene structure is required.

In [42] an innovative technique using Game Theory approach for identifying digital camera is discussed. The aim is to detect fingerprint-re-create attack, when an adversary uses copy of original camera'due south fingerprint. Therefore, this problem is represented as an interplay between sensor-based camera identification and the fingerprint-re-create assault. A Bayesian game is used for analyzing differences between original camera'due south fingerprint and the fingerprint-re-create. The Nash equilibrium is used to evaluate the efficacy of proposed method.

In [33] there is proposed an approach for identifying a camera with the employ of enhanced Poissonian-Gaussian model. This model describes distribution of pixels in a RAW epitome. Cameras' fingerprints are represented as parameters of a statistical noise of considered model. Experiments are conducted with Dresden Image Database and also authors' own image fix.

In [37] trouble of image splicing is considered. It is assumed that image splicing tin be detected by analyzing noise level in spliced parts. It turns that splicing parts have different level of noise, what causes racket inconsistencies between them. This in turn allow for detecting the activeness of splicing. A racket level function (NLF) is used. Experimental evaluation confirms efficacy of the NLF estimation. Piece of work [37] is an extension of [33], where inconsistencies of images spliced regions are examined. Due to limitations of standard solution for estimating dissonance variance of each region, authors advise to use scoring strategy. An paradigm is divided into small patches and the noise variance is calculated by kurtosis concentration-based pixel-level racket estimation method. Then, a sample of the racket variance and a inhomogeneity score of each region is fitted by a linear function. Experimental results confirmed efficacy of proposed method.

In [38] the problem of managing a large database of camera fingerprints is considered. Cameras' fingerprints are represented as matrices of the noise whose resolution is equal to photographic camera's produced epitome size. A creature-forcefulness searching a specified fingerprint in a big database of N fingerprints takes O(n N), where n is the number of pixels in each fingerprint. Therefore, the goal is to reduce this time. In considered paper a fast search algorithm is proposed. Algorithm extracts a digest of the query fingerprint of the 10,000 fingerprint values and approximately matches their positions with positions of pixels in the digests of all database fingerprints. In the worst case, the complexity of this algorithm still could be the aforementioned as the database size, just in practice it is much faster. Experiments showed that for ii-megapixel fingerprints searching takes 0.ii of second. However, this approach has some serious limitations. Present, cameras' prototype sensors are much bigger than two-megapixels therefore search time will again increase. Secondly, this approach deals with searching the existing fix of cameras' fingerprints, Therefore it is required to take such fingerprint set. This is nonetheless non practical due to big sizes of recent cameras sensors, where for instance for 24-megapixel sensor, the fingerprint however must be a matrix with a corresponding size.

In [sixteen] a method for photographic camera identification is discussed. Computing camera's fingerprint is in the similar spirit as in [31]. Evaluation is fabricated using the Peak to Correlation Energy ratio (PCE). Experiments are very representative, images are utilized from the popular on-line prototype sharing site Flickr. Tests included more than million images of 6896 cameras covering 150 models. In [15] the same problem is solved by using support vector machines (SVM) with decision fusion techniques.

Analysis of vignetting and lens baloney

In this department we consider artifacts of vignetting and lens distortion in order to recognize camera's brand. In both cases an image is represented according to the \(\mathcal {R}\mathcal {1000}{B}\) model as M × Due north by iii information array that defines red, light-green and bluish colour components for each private pixel.

Vignetting-CT algorithm

Equally mentioned in the Introduction, vignetting is a defect depending on reduction of brigthness at the prototype frame, normally in its corners. The easiest way to observe the presence of vignetting is a photo of evidently surface (Fig. 1).

Fig. 1

Case of image of a patently surface. The pixel intensity in the heart of the image is 94; average pixel intensities in corners a _one, a ₂, a ₃, a _iv are respectively: 74,72,84,85

Full size paradigm

We propose a procedure called Vignetting-Camera Tracing (Vignetting-CT) for calculating the differences of pixel intensities in prototype corners (Algorithm ane ).

Vignetting-CT algorithm is very elementary and comes to split up an image into iv "pocket-size" parts at its corners and to summate mean values of pixel intensities expressed in \(\mathcal {RGB}\) note. This algorithm tin be performed for any color channel, merely we suggest to process blood-red (\(\mathcal {R}\)) color channel (line 1). Side by side step is median filtering of this aqueduct (line two) and computing the rest S defined as an absolute difference of the color channel and its median-filtered form (line 3). The d parameter defines size of image parts that are to be analyzed (lines iv, five). We advise to apply d = 0.05. So, hateful values of pixel intensities in image corners are calculated (lines 6-9). Finally, nosotros compute hateful value of pixel intenisties \(\chapeau {d}\) in corners of residual S (line ten). We suggest the \(\lid {d}\) value to apply as a fingerprint for recognizing camera'south brand. Sample division of image frame is presented in Fig. 1.

Worth noticing that operating on Southward reveals the vignetting even, if epitome is not blank. We have inspected in detail pixel intensities of rest S and it turns that in most images average pixel intensity of whole S is brighter than for considered corners. Sample image is presented in Fig. 2. Sample values for some photos from Nikon D70s (i) are presented in Table i.

Fig. 2

Sample image and its residuum Due south calculated as accented difference of an prototype and its median-filtered version. Average value of pixel intensities in S is 0.half-dozen, intensities in corners in S: \(\hat {s_{a_{1}}} = 0.36\), \(\hat {s_{a_{2}}} = 0.49\), \(\hat {s_{a_{3}}} = 0.34\), \(\chapeau {s_{a_{four}}} = 0.54\)

Total size epitome

Tabular array 1 Sample vignetting values for Nikon D70s (1) in residue S

Full size table

We propose to apply median filter instead of wavelet-based denoising filter that is mainly used for denoising images [18, 21, 31]. Median filtering is noticeably faster than wavelet-based denoising. Vignetting-CT algorithm is computationally effective, its complexity is O(m north), where m and n define the size of image parts for calculating pixel intensities. Due to small values of m and n, calculations are carried out very apace.

Lens distortion

Distortion is a kind of defect of irresolute geometry of the paradigm transmitted past lens to camera'south photosensitive sensor, particularly closer to the corners and edges of the image frame. Essential for calculating distortion is the employ of calibration grid which consists of crossing vertical and horizontal lines [5]. Such grid is used to compare it with lines in the image. If the lines in the image embrace with the grid, there is no baloney in the photo. Otherwise, there is a barrel or pincushion distortion. Barrel distortion appears when image magnification decreases with distance from the optical axis. It often appears in pictures taken with wide-angle lenses. Prototype elements wait equally they were bent outside the image. Similarly, in pincushion baloney image magnification increases with distance to the optical axis. An paradigm seems to be squeezed within the center of the frame. A sample photo with visible butt baloney is presented in Fig. 3.

Fig. 3

Paradigm with distortion and the filigree of horizontal and vertical lines. Scarlet lines denote distorted points

Full size prototype

In literature there are many models that draw lens baloney. Most common are polynomial models [seven, 14]. Nosotros propose a model defined every bit (1). This model is a simplified version of Brown's model [7].

$$ p_{u} = p_{d}(1+kr^{2}) $$

(ane)

where:

• p _u (x _u , y _u ) – undistorted image signal;

• p _d (x _d , y _d ) – distorted image betoken;

• m – distortion parameter;

• \(r = \sqrt {(x_{d} - x_{u})^{two}+(y_{d} - y_{u})^{2}}\).

We propose to calculate the distortion parameter grand for a fix of images of different cameras and cheque if there are some tendences that might be helpful to be used in order to recognize a specific camera. The p _u and p _d tin be determined past using software (for example Hugin Photo Stitcher [19]) or manually. Knowing distorted and undistorted points, this procedure leads for solving (1), where k is unknown. Of course, for a set of distorted and corresponding undistorted points there will be the same number of k values that might be unlike. In such instance nosotros propose to boilerplate of all k values.

Permit us consider a simple toy example in which we show the reasoning of computing the value of baloney.

Example ane (Toy instance)

Suppose that we have coordinates of the following set of distorted p _d and respective undistorted p _u points: \(p_{d_{ane}} = (100,80)\), \(p_{u_{1}} = (110,90)\) \(p_{d_{two}} = (210,100)\), \(p_{u_{two}} = (200,110)\) \(p_{d_{iii}} = (215,177)\), \(p_{u_{three}} = (217,184)\) We calculate r ₁, r ₂ and r ₃. \(r_{1} = \sqrt {(x_{d_{1}} - x_{u_{1}})^{two}+(y_{d_{1}} - y_{u_{i}})^{two}} = \sqrt {(100-110)^{2}+(80-ninety)^{2}} = xiv.14\) Similarly, r ₂ = fourteen.14 and r _three = 7.28 Inserting into (1) and calculating the k values for \(p_{d_{1}}\) and \(p_{u_{1}}\): 100 = 110(ane + grand · 14.fourteen) k ₁₍₁₎ = ––0.09 80 = ninety(1 + k · 14.14) k ₁₍₂₎ = 0.07 Similarly, for side by side pair of points \(p_{d_{two}}\), \(p_{u_{2}}\) and \(p_{d_{3}}\), \(p_{u_{3}}\) 1000 ₂ = –0.003 and 0.007; k ₃ = 0.001 and –0.005 Finally, nosotros calculate the hateful value of all chiliad values: \(k = \frac {-0.09+0.07+(-0.003)+0.007+0.001+(-0.005)}{6} = -0.003\) Thus, the k = –0.003 is the searched parameter.

In a higher place process should be performed for all images separately. We propose to consider the k parameter as unique that might exist used to distinguish cameras. Due to simplicity, proposed process is fast and can be easily implemented.

Experimental verification

In this section we compare results of recognizing cameras' brands by analyzing \(\lid {d}\) value of Vignetting-CT and thousand baloney parameter with Lukás et al.'s algorithm [31] in terms of efficiency of classification and time performance. Details of Lukás et al.'due south algorithm are recalled in the I. For evaluation of this algorithm, nosotros apply original authors' MATLAB implementation [30]. Both Vignetting-CT algorithm and script for calculating distortion parameter k are implemented in MATLAB.

Nosotros use the accuracy (ACC), divers in the standard way as an evaluation statistic:

$$ \text{ACC} = \frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}}~, $$

where TP/TN denotes "true positive/true negative"; FP/FN stands for "false positive/false negative". TP denotes number of cases correctly classified to a specific class; TN are instances that are correctly rejected. FP denotes cases incorrectly classified to the specific class; FN are cases incorrectly rejected.

Devices

Experiments are conducted on two datasets. First dataset contains images from popular smartphones (farther chosen "smartphones dataset"). We have used 264 JPEG images from 12 smartphones. Used smartphones include: Apple iPhone 6, Asus ZenFone two, HTC 1 M9, Huawei P8, LG G3, LG G4, Lumia 1020, Lumia 1520, Samsung Galaxy Notation four, Samsung Galaxy S6, Sony Xperia Z3 and Sony Xperia Z3+. All devices contain CMOS sensors. 2nd dataset include images from the Dresden Paradigm Database [ix]. This database consists of tens of thousands images fabricated past different cameras and is often used for research [8, 12]. We take used 11787 JPEG images of 48 cameras. Used cameras include: Agfa DC 733s, Agfa DC 830i, Agfa Sensor 505, Agfa Sensor 530s, Canon Ixus 55, Canon Ixus 70 (3 devices), Casio EX Z150 (5 devices), Kodak M1063 (5 devices), Nikon CoolPix S710 (5 devices), Nikon D70 (ii devices), Nikon D70s (ii devices), Nikon D200 (two devices), Olympus 1050SW (5 devices), Praktica DCZ5 (v devices), Rollei RCP 7325XS (iii devices), Samsung L74 (3 devices) and Samsung NV15 (3 devices). In well-nigh cases, images were taken of the same paradigm frames by unlike devices. All cameras in this dataset contain CCD sensors. In cases of both datasets all images are JPEG lossy compressed and come up directly from cameras. We do non assume further processing of images, for case user'south graphic processing.

Experiment I – brand identification by analyzing vignetting

We analyze influcence of underexposed areas in the corners of images for recognizing the camera. Experiments are performed in the following way. The \(\lid {d}\) value is calculated for every image from each camera and mean value of \(\hat {d}\) of images from a specific photographic camera is calculated. To classify a new epitome K, its \(\lid {d}_{K}\) is calculated. Obtained effect is assigned to the closest mean \(\hat {d}\) from a specific camera and assumed as taken by this camera.

For smartphones dataset the \(\lid {d}\) value has been calculated for 22 images per device. Results of classification are presented in Tables 2, 3, iv, v.

Table 2 Defoliation matrix of model recognition, Vignetting-CT, smartphones dataset, ACC = 0.62

Full size table

Tabular array three Confusion matrix of brand recognition, Vignetting-CT, smartphones dataset, ACC = 0.72

Full size table

Table 4 Confusion matrix of model recognition, Lukás et al.'south algorithm, smartphones dataset, ACC = 0.84

Total size tabular array

Table 5 Confusion matrix of brand recognition, Lukás et al.'s algorithm, smartphones dataset, ACC = 0.84

Full size tabular array

For Dresden Epitome Database the \(\lid {d}\) value has been calculated for at to the lowest degree 180 images per device. Results of make nomenclature are presented in Tables 6 and 7. For the clarity, we exercise not present results for model classification, due to the amount of 48 cameras.

Table 6 Confusion matrix of make recognition, Vignetting-CT, Dresden Image Database, ACC = 0.52

Full size table

Tabular array 7 Confusion matrix of brand recognition, Lukás et al., Dresden Image Database, ACC = 0.83

Full size tabular array

Results presented in defoliation matrices signal that camera's brand classification is noticeably higher for Lukás et al.'s algorithm. In cases of two tested datasets the accuracy of make classification is 84% for smartphones dataset and 83% for Dresden Prototype Database. Efficiency of Vignetting-CT algorithm is 72% for smartphones dataset and 52% for Dresden Prototype Database. Advantage of Lukás et al.'due south algorithm is classification "stability", what is especially visible in defoliation matrices of brand recognition.

It is worth saying that Lukás et al.'south algorithm achieves better performance in example of older devices with CCD sensors. In [2] it was shown that performance of this algorithm is lower for newer cameras with CMOS sensors. Nowadays, recent cameras have CMOS sensors instead of CCDs.

Time performance

Data presented in Table 8 and Fig. four clearly betoken that Lukás et al.'s algorithm is defeated in terms of fourth dimension of epitome processing. Vignetting-CT algorithm processes images in real time, while Lukás et al.'s takes at boilerplate almost 90 seconds to process a single prototype. Of course, image processing time is dependent on the prototype resolution. Lower resolution images (e.g. 6 megapixels 3000x2000px) are processed with less than 1 minute, yet, 24 megapixels images of resolution 6000x4000px are candy most iv minutes. To sum up, the whole time for processing 12051 images took less than 40 minutes in instance of Vignetting-CT algorithm and well-nigh 294 hours for Lukás et al.'s algorithm. Such poor fourth dimension performance excludes usage of Lukás' algorithm for a mass acale. In [36] it was examined if the image processing time Lukás' algorithm could be decreased by processing small fragments of images. For this purpose 50×50 pixels fragments of photos were used, however the results of classification were non satisfactory.

Table 8 Processing fourth dimension of smartphones dataset and Dresden Image Database (12051 photos in total)

Total size table

Fig. 4

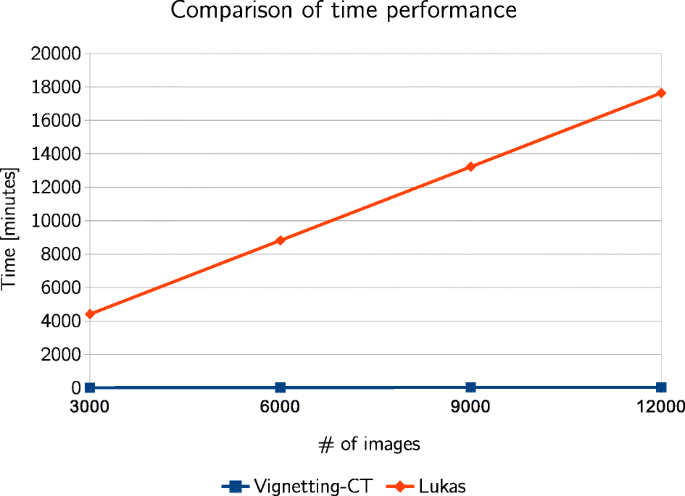
Comparison of time performance of Lukás et al.'south algorithm and Vignetting-CT for all images (12051)

Full size epitome

The experiments were conducted on MSI GV62-7RD notebook with quad-core Intel Core i5-7300HQ processor with 24GB of RAM. It is worth mentioning that camera'due south fingerprint in Lukás et al.'s algorithm is stored equally a matrix of size of camera'south images. Authors' implementation produces the fingerprint files as MATLAB *.mat files which are usually of weight at least 110 megabytes. It ways that calculated fingerprints for 2 used datasets of over 12 k of images weigh about 1.two terabyte.

Experiment II – comparison of lens baloney

Nosotros clarify lens distortion parameter thousand for images from dissimilar devices but for the same prototype frames. Script for computing m parameter was written in MATLAB, but information technology can also be used the Hugin Photo Stitcher software [19] that measures the distortion. We have compared distortion results from MATLAB script with Hugin software and obtained results are the same. Analysis shows that despite photographing the same scene, distortion parameter appears to be different for diverse devices. Sample results are presented in Figs. 5 and 6. It is worth mentioning that dissimilar devices of the same photographic camera model give different values of k parameter. Such example is presented in Fig. 5, where the aforementioned image frame of two unlike smartphones (Huawei P8 and Samsung S6) generates unlike distortion parameters. A similar state of affairs is presented in Fig. half-dozen, for two different devices of Nikon CoolPix S710 (Dresden Paradigm Database).

Fig. 5

Lens distortion of images of the same frame, smartphones dataset. Paradigm (ane) (Huawei P8), distortion parameter k = –0.6782; prototype (two) (Samsung S6), distortion parameter yard = –0.ii

Total size image

Fig. 6

Lens distortion of images of the same frame, Dresden Image Database. Image (1) (Nikon CoolPix S710 (device #ii)), distortion parameter yard = –0.10323; prototype (2) (Nikon CoolPix S710 (device #0)), distortion parameter thousand = –0.01799

Total size epitome

Sample results of k distortion parameter are presented in Tables nine and x. Due to large number of devices and images, nosotros present for the clarity only function of full results. It is visible that all photos taken past diverse devices have unlike distortion parameters. Therefore proposed approach gives information if a ready of images was done past i or more cameras, even so it tin can not exist used to decide of what model or even brand was used. What is more, an advantage of proposed method is its speed, because distortion parameter k is calculated in real time. Moreover, there are many applications that calculate and correct lens distortion in photos, thus at that place is no need to implement distortion algorithm manually. Of course proposed method can be useful in simple cases of comparing like photos, notwithstanding information technology may not be practical for sets of dissimilar images. One of the reason is that distortion parameter changes due to distance to the object, angle of view and focal length.

Table ix Sample values of k lens distortion parameter of the same image frame for dissimilar sample devices, smartphones dataset

Full size table

Table x Sample values of 1000 lens baloney parameter of the aforementioned image frame for different sample devices, Dresden Image Database

Full size table

Summary

We have analyzed influence of vignetting and lens distortion defects to the problem of digital camera recognition. Experiments show that assay of vignetting can be used for brand recognition. Compared to Lukás et al.'s algorithm, model recognition is lower, however Vignetting-CT algorithm beats Lukás et al.'southward algorithm in terms of speed. Efficiency of brand recognition on smartphones dataset and Dresden Image Database is 72% and 52%, respectively, while Lukás et al.'southward algorithm achieves 84% and 83%. Even so, an advantage of Vignetting-CT algorithm is processing images in real fourth dimension, while Lukás et al. takes at average about 90 seconds per photo. Therefore, the Lukás et al.'southward algorithm needed more than 290 hours to calculate cameras fingerprints, what excludes this algorithm of usage for a mass scale.

We take also experimentally shown that analysis of lens distortion can be useful to distinguish if a set of images of the same frame was taken past the same camera. Photos of the same frame just made with diverse cameras generate different distortion parameters. Of course, such arroyo may be not applied for camera recognition in instance of images of different frames, nevertheless information technology can be useful for analysis of similar photos. The main disadvantage of baloney is its heterogenity. Baloney changes due to altitude to the object, focal length or angle of view, therefore there is probably no possibility to suggest reasonable model that could exist used for tracing cameras for a mass scale. Another limitation is that if there are no straight lines in the motion picture, distortion can non be adamant.

Conclusion and futurity work

In this paper the problem of recognizing digital cameras by photographs was examined. Most popular solutions are based on denoising images with wavelet-based denoising filter and computing so-called sensor pattern noise which averaged gives camera's fingerprint. We take proposed a novel arroyo for tracing digital cameras by analysis of vignetting and distortion defects. We have compared obtained results with state-of-the-fine art Lukás et al.'s algorithm. Experiments have shown that despite lower efficiency it is possible to recognize brand of the camera by analysis of vignetting defect. Our approach defeats the Lukás et al.'due south algorithm in terms of image processing time. Proposed Vignetting-CT algorithm processes images in existent fourth dimension, while Lukás et al.'s algorithm needs at average xc seconds to calculate the sensor pattern noise of one photograph. Moreover, Vignetting-CT algorithm does not crave calculating cameras' fingerprints what is very time consuming. Analysis of distortion showed that images of different devices (also of the same model) generate different distortion parameters. Therefore, there is a possibility to distinguish if photos were taken past the same camera. This method is useful for a set of similar images and is very fast as well calculating distortion parameter is performed in real fourth dimension.

Future works will business organisation further experiments with lens distortion analysis. It should be examined if it is possible to advise a model of distortion that could be used for reliable and more universal camera recognition. Information technology would even be interesting to bank check if other optical defects like chromatic or spherical aberration would be useful to trace the camera's brand. Moreover, we are going to cheque efficiency of Vignetting-CT algorithm with classifiers based on Deep Learning or Convolutional Neural Networks approaches.

References

1. Baar T, van Houten Westward, Geradts Z (2012) Camera identification by grouping images from database, based on shared dissonance patterns. CoRR abs/1207.2641

2. Bernacki J, Klonowski 1000, Syga P (2017) Some Remarks about tracing digital cameras – faster method and usable countermeasure. In: Proceedings of the 14th International Articulation Briefing on e-Business and Telecommunications (ICETE 2017), pp 343–350

3. Bloy GJ (2008) Bullheaded camera fingerprinting and image clustering. IEEE Trans Pattern Anal Mach Intell 3:xxx

   Google Scholar

4. Chapman GH, Thomas R, Thomas R, Koren Z, Koren I (2015) Enhanced correction methods for loftier density hot pixel defects in digital imagers

5. Claus D, Fitzgibbon AW (2005) A rational function lens distortion model for general cameras. In: Proceedings of the 2005 IEEE Estimator Club Conference on Computer Vision and Blueprint Recognition (CVPR'05)

6. De Silva V, Chesnokov V, Larkin D (2016) A Novel Adaptive Shading Correction Algorithm for Camera Systems, Electronic Imaging, Digital Photography and Mobile Imaging XII, pp one–5(5)

   Article  Google Scholar

7. de Villiers JP, Leuschner FW, Geldenhuysm R (2008) Centi-pixel accurate existent-fourth dimension changed distortion correction, 2008 International Symposium on Optomechatronic Technologies. SPIE. https://doi.org/x.1117/12.804771

8. Deng Z, Gijsenij A, Zhang J (2011) Source camera identification using auto-white residuum approximation. In: 2011 IEEE International Briefing on Computer Vision (ICCV), pp 57–64

9. (2008) Dresden Prototype Database. http://forensics.inf.tu-dresden.de/ddimgdb/ Online; accessed 3 December 2018

10. Fuentes L, et al. (2015) Revisiting Image Vignetting Correction by Constrained Minimization of Log-Intensity Entropy Volume 9095 of the book series Lecture Notes in Computer science (LNCS)

11. Galdi C, Nappi Thou, Dugelay J (2016) Multimodal authentication on smartphones: combining iris and sensor recognition for a double bank check of user identity. Design Recogn Lett 82:144–153

    Article  Google Scholar

12. Gloe T (2012) Feature-based forensic photographic camera model identification. LNCS Transactions on Data Hiding and Multimedia Security (DHMMS), to appear

13. Goljan Chiliad (2008) Digital camera identification from images - estimating faux acceptance probability. In: Digital Watermarking, 7th International Workshop, IWDW 2008, pp 454–468

    Chapter  Google Scholar

14. Goljan M, Fridrich J (2014) Interpretation of lens distortion correction from single images. In: Proceedings volume 9028, media watermarking, Security, and Forensics 2014; 90280N

15. Goljan M, Fridrich J, Filler T (2009) Big scale test of sensor fingerprint camera identification, In: Proceedings of SPIE - The International Social club for Optical Applied science, https://doi.org/10.1117/12.805701

16. Goljan Yard, Fridrich J, Filler T (2010) Managing a Large Database of Camera Fingerprints, In: Proceedings of SPIE - The International Society for Optical Applied science, https://doi.org/10.1117/12.838378

17. Goljan One thousand, Fridrich JJ, Chen M (2011) Defending confronting fingerprint-re-create attack in sensor-based camera identification. IEEE Trans Inf Forensics Secur 6(1):227–236

    Article  Google Scholar

18. Hu Y, Li C-T, Lai Z, Zhang South Fast photographic camera fingerprint search algorithm for source camera identification. In: Proceedings of the 5th International Symposium on Communications, Control and Signal Processing, ISCCSP 2012, Rome, Italian republic, 2-iv May 2012

19. Hugin Photo Stitcher http://hugin.sourceforge.net/, last admission four December 2018

20. Julliand T, Nozick V, Talbot H (2016) Image Noise and Digital Prototype Forensics. Springer International Publishing, Cham, pp 3–17

    Google Scholar

21. Kang 10, Li Y, Qu Z, Huang J (2012) Enhancing source camera identification performance with a photographic camera reference phase sensor pattern dissonance. IEEE Trans Inf Forensics Secur 7(2):393–402

    Article  Google Scholar

22. Khan MB, Nisar H, Ng CA, Lo PK (2016) A vignetting correction algorithm for Bright-Field microscopic images of activated sludge. In: 2016 International Conference on Digital Image Computing: Techniques and Applications (DICTA)

23. Kordecki A, Bal A, Palus H (2016) Local polynomial model: a new arroyo to vignetting correction. In: Proc SPIE 10341 Ninth International Conference on Automobile Vision

24. Kordecki A, Bal A, Palus H (2016) A report of vignetting correction methods in camera colorimetric calibration. In: Proc SPIE 10341 9th International Briefing on Automobile Vision

25. Kordecki A, Palus H, Bal A (2016) . Practical vignetting correction method for digital camera with measurement of surface luminance distribution 10(8):1417–1424

    Google Scholar

26. Lanh TV, Chong K, Emmanuel S, Kankanhalli MS (2007) A survey on digital camera image forensic methods. In: Proceedings of the 2007 IEEE International Conference on Multimedia and Expo, ICME, 2007, pp 16–19

27. Lee SY, Cho HJ, Lee HJ (2016) Method for vignetting correction of image and apparatus therefor US 20160189353 A1

28. Li H, Hartley R (2005) A Non-iterative Method for Correcting Lens Baloney from Nine Bespeak Correspondences, In: Proc OmniVision'05, ICCV-workshop

29. Li 10, Shen H, Zhang L, Zhang H, Yuan Q (2014) Dead pixel completion of aqua MODIS band 6 using a robust m-calculator multiregression. IEEE Geosci Remote Sensing Lett xi(four):768–772

    Commodity  Google Scholar

30. Lukas J, Fridrich JJ, Goljan M (2016) Matlab implementation

31. Lukás J, Fridrich JJ, Goljan G (2006) Digital camera identification from sensor pattern dissonance. IEEE Trans Inf Forensics Secur i(2):205–214

    Article  Google Scholar

32. Park S-W, Hong Chiliad-Southward (2001) Applied ways to calculate camera lens distortion for real-time photographic camera scale. Blueprint Recogn 34:1199–1206

    Article  Google Scholar

33. Qiao T, Retraint F (2018) Identifying private photographic camera device from RAW images, digital object identifier, vol 6, pp 78038-78054 IEEE Admission, https://doi.org/10.1109/Admission.2018.2884710

    Commodity  Google Scholar

34. Ray SF (2002) Practical photographic optics, 3rd ed. Focal Press ISBN 978-0-240-51540-iii

35. Schwarting Grand, Burton T, Yampolskiy R (2016) On the obfuscation of image sensor fingerprints, 2015 annual global online conference on information and figurer technology IEEE

36. Taspinar South, Mohanty M, Memon ND (2016) PRNU Based source attribution with a collection of seam-carved images. In: 2016 IEEE International Briefing on Image Processing, ICIP, pp 156–160, vol 2016

37. Yao H, Wang South, Zhang 10, Qin C, Wang J (2017) Detecting image splicing based on noise level inconsistency. Multimed Tools Appl 76:12457–12479

    Article  Google Scholar

38. Yao H, Cao F, Tang Z, Wang J, Qiao T (2018) Expose noise level inconsistency incorporating the inhomogeneity scoring strategy. Multimed Tools Appl 77:18139–18161

    Article  Google Scholar

39. Zheng Y, Lin South, Kambhamettu C, Yu J, Kang SsB (2009) Single-Image Vignetting correction. IEEE Trans Pattern Anal Mach Intell 31(12):2243–2256

    Article  Google Scholar

40. Zheng Y, Lin South, Kang SB, Xiao R, Gee JC, Kambhamettu C (2013) Single-Image Vignetting correction from gradient distribution symmetries. IEEE Trans Pattern Anal Mach Intell 35(6):1480–1494

    Article  Google Scholar

41. Zeng H, Chen J, Kang X, Zeng W (2015) Removing photographic camera fingerprint to disguise photograph source. In: 2015 IEEE International Conference on Epitome Processing, ICIP 2015, Quebec City, QC, Canada, September 27-30, 2015, IEEE, pp 1687–1691

42. Zeng H, Liu J, Yu J, Kang South (2017) A framework of camera source identification bayesian game. IEEE Transactions on Cybernetics 47(7):1757–1768

    Article  Google Scholar

Download references

Author information

Authors and Affiliations

1. Częstochowa University of Technology, al. Armii Krajowej 36, 42-200, Częstochowa, Poland

   Jaroslaw Bernacki

Corresponding author

Correspondence to Jaroslaw Bernacki.

Additional information

Publisher's notation

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Lukás et al.'southward algorithm

Appendix: Lukás et al.'s algorithm

Lukás et al. in [31] proposed an algorithm for identifying digital camera by produced images. This algorithm extracts a specific pattern called the photo-response nonuniformity dissonance (PRNU) which serves equally a unique camera's identification fingerprint. Algorithm extracts noise from input image P by using a denoising filter F. Then, camera's fingerprint is calculated every bit C = P - F(P).

Input: Prototype P in RGB of size M × N; Output: Matrix C of noise residue, size M × N.

1. one.

   Calculate \(M=\frac {P_{\mathcal {R}} + P_{\mathcal {G}} + P_{{\mathscr{B}}}}{3}\);

2. 2.

   Denoise all channels of input paradigm \(P_{\mathcal {R}}\), \(P_{\mathcal {G}}\), \(P_{{\mathscr{B}}}\) with filter F;

3. 3.

   Calculate mean \(D = \frac {F(P_{\mathcal {R}}) + F(P_{\mathcal {One thousand}}) + F(P_{{\mathscr{B}}})}{3}\);

4. iv.

   Summate matrix of noise rest: C = K - D.

where \(P_{\mathcal {R}}\), \(P_{\mathcal {K}}\) and \(P_{{\mathscr{B}}}\) are matrices of each component of RGB model of input P; F is the denoising filter. For denoising, authors advise using the wavelet-based denoising filter.

Authors suggest to use at least 45 images from each camera to summate the PRNUs for each paradigm and and so average obtained PRNUs, what as a result will give photographic camera's fingerprint.

Rights and permissions

Open up Access This article is distributed under the terms of the Creative Eatables Attribution iv.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted utilise, distribution, and reproduction in any medium, provided yous requite advisable credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and Permissions

Nearly this article

Cite this article

Bernacki, J. Digital camera identification based on assay of optical defects. Multimed Tools Appl 79, 2945–2963 (2020). https://doi.org/10.1007/s11042-019-08182-z

Download commendation

• Received: 12 December 2018

• Revised: 09 June 2019

• Accustomed: 02 September 2019

• Published: 04 December 2019

• Issue Appointment: January 2020

• DOI : https://doi.org/10.1007/s11042-019-08182-z

Keywords

• Hardwaremetry
• Camera recognition
• Sensor identification
• Photograph response not uniformity
• Distortion
• Vignetting
• Privacy
• Digital forensics

Source: https://link.springer.com/article/10.1007/s11042-019-08182-z

Posted by: johnwasion.blogspot.com

Share this post